The Heat Transfer Process
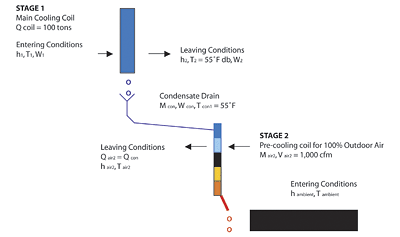
Figure 1 will be used throughout this article to analyze the psychrometrics of recovering heat from the low enthalpy condensate. When air is cooled below its dewpoint, moisture is released at constant temperature conditions. Heat transfer between the metal of the coil and the moisture droplets is governed by conduction. At the microenvironment of the heat exchanger, the temperature of the condensate discharged from the evaporator coil will approach the coil surface temperature. In hot and humid summer seasons, the enthalpy of this condensate is low enough to be utilized in a heat recovery process.
The process described above is analyzed in two stages. The first stage analysis is the main cooling load and the second stage is the separate heat recovery precooling load. The process is most economical and makes most sense if the first stage latent cooling load is large enough to generate considerable condensate flow, the climate is humid throughout the year (high summer wetbulb temperatures), and the condensate from the first stage coil is drained by gravity to the heat recovery pre-cooling coil (second stage to save on additional pump horsepower).
Psychrometric Cycles
Two basic heat balance equations govern the heat transfer and condensation process of a cooling coil.
The steady-flow energy equation:
(1) Qcoil = Mair1 (h1 - h2)
and mass balance equation:
(2) Mcon = Mair1 (w2-w1)
Where,
Qcoil = The cooling load of the cooling coil in Btu.
Mcon = The condensate that results from the cooling of the airstream below its dewpoint (lb).
h = Enthalpy and grains of moisture per pound of air (Btu/lb).
w = Grains of moisture per pound of air.
T = Temperature in °F.
Adding time to both equations yields the rates of heat flow and condensate flow.
Let this condensate discharge by gravity to another coil, which is placed in a second incoming airstream Mair2 totally independent of the first airstream cycle. The temperatures of the condensate entering and leaving the second cooling coil are designated as Tcon1 and Tcon2. Therefore the heat flow rate equation at the second coil is:
(3) Qcon = Mcon Cp (Tcon1-T2con)
Where Cp is the specific heat of water.
Assuming no external heat gain or loss of the condensate, the heat balance equations between the condensate and the second airstream must balance since the heat lost by the higher enthalpy airstream is gained by the lower enthalpy condensate in the coil. Therefore:
(4) Qcon = Qair2
and
(5) Qair2 = Qcon = Mair2 x (hamb-hair2)
If we know the quantity of air in the second airstream, we may then solve for hair2:
(6) hair2 = hamb - (Qcon / Mair2)
Applying the above equations to a simple air conditioning process with chilled water as the refrigerant fluid, at standard atmospheric pressure conditions, a psychrometric chart can be used to extrapolate data. Air is cooled to saturation at 55°F. Ambient conditions are chosen for 0.4% ASHRAE values, and the derived equation for flow from equation (3) in gallons per minute (gpm) and Heat loss/Heat gain (Q) from equation (6) in Btuh are assumed to be widely familiar by HVAC engineers in the form:
(7) gpm = Q
490 x (T2-T1)
(8) Q = cfm x 4.5 x (h2-h1)
Stage 1. Main cooling and dehumidification. An air handler has the capacity to cool a volumetric flow rate of outside air "V" (in cfm) from maximum summer ambient conditions down to 55° saturation. Since mass flow rate is conserved, volumetric flow rate is converted to mass flow rate by dividing by the specific volume and converting from hours to minutes. Using the psychrometric chart, all the entering and leaving conditions including enthalpy and grains of moisture per pound of air are extrapolated. The condensate flow rate, Mcon, in pound per minute is obtained from equation (2).
Stage 2. Heat recovery load. The condensate Mcon is piped to another coil totally separate from the first stage. A volumetric flow rate, Vair2, at maximum summer ambient conditions is passed through the coil. Entering conditions for both the condensate and the air are known. If a theoretical maximum heat transfer occurs at the coil, the leaving water temperature will approach the incoming airstream temperature (equal to the maximum summer ambient). The leaving condensate conditions are now known, and equation (7) is used to calculate the cooling capacity of the condensate coil Qcon.
The heat gained by the condensate is equal to the heat lost by the incoming airstream from equation (4). Substituting Qcon for Qair2 in equation (6), the leaving enthalpy of the outdoor air is calculated. The final enthalpy of the second airstream has been lowered by contacting it with condensate from a previous coil process.
Apart from enthalpy, which was mathematically calculated, the final condition of the second airstream is still unknown. The second airstream did experience a lowering of temperature and moisture content, however, the conditions of the airstream will not reach saturation unless the flow rate of the condensate from stage one is large enough. It is concluded that since Mcon, Tcon from the first stage are constants, we can achieve maximum pre-cooling of the second airstream if more condensate Mcon is discharged from the first airstream (e.g., a very large primary latent load), and if the mass flow rate of the second air stream is small.
Example and Discussion
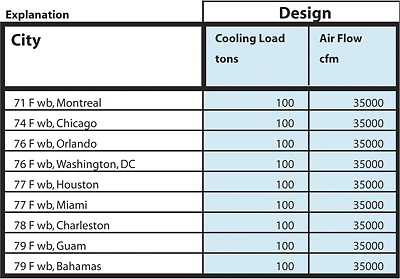
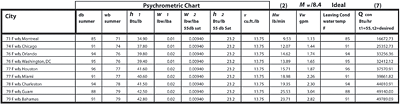
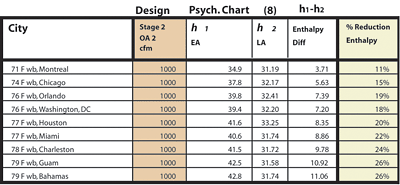
The following example is an application of the above analysis. Several locations with varying wetbulb temperatures are chosen. They are Washington, Orlando, Houston, Chicago, Guam, Montreal, and the Bahamas. Standard atmospheric conditions are assumed. Grains of moisture per pound of dry air are extrapolated from a psychrometric chart.A standard1 stage one primary air conditioning cooling tonnage is chosen at 100 tons, 35,000 cfm, and a stage two secondary 100% outdoor air is chosen for all cities at 1,000 cfm (Figure 1). Condensate from stage one enters a pre-cooling coil stage two at 55°. The pre-cooling coil is designed so that the leaving temperature of the condensate (designated as Tcon2) approaches the incoming air drybulb (Tambient in this case). Equating the heat gained by the condensate to the heat lost by the ventilation airstream, the leaving air enthalpy hair2 is calculated from equation (8). Equation variables and the percentage reduction in enthalpy are shown in Table 1.
Table 1 reveals that for any of the locations, there was a reduction in the leaving air enthalpy. The reduction in enthalpy ranges between 26% and 18% for most locations and drops further as wetbulb decreases. The percentage reduction is directly related to wetbulb temperature.
Ultimately, the reader is interested in the maximum load reduction as a result of using the cold condensate to pre-cool the airstream. Table 2 shows the loads for two conditions; the enthalpy of saturation minus the enthalpy of the airstream with and without the pre-cooling coil. Using equation (8), the total load for each condition is calculated.
The percentage reduction in load for cities with wetbulbs as low as 76° ranges between 56% and 45% at peak summer wetbulb conditions. The percentage reduction in the load drops with wetbulb temperature particularly below 76°. Nevertheless, there is a significant amount of heat recovery from the low enthalpy condensate for a wide range of locations. Again, the percentage reduction is directly proportional to wetbulb. One interesting observation is noted. Table 2 shows that certain cities further south, such as Orlando, have equal wetbulb temperatures to Northern cities such as Washington. The percentage reduction for Washington is almost the same as Orlando. This observation shows that the analysis should weigh more on wetbulb temperature rather than geographic location.
What this paper does not touch upon is the duration of the wetbulb temperature throughout the year. Orlando, in this instance, might have a higher wetbulb temperature occurrence throughout the year than Washington. The cost-benefit of installation could be more economically justifiable for projects in Orlando rather than Washington.
Sensitivity Analysis
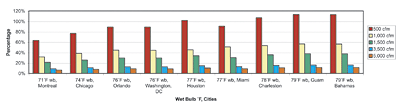
While maintaining the primary stage cooling load constant at 100 tons, the secondary stage outdoor air cfm is varied. The percentage reduction in load is calculated for each outdoor airflow rate. The results are shown in Table 3 and Figure 2. A 50% reduction from the base 1,000 cfm down to 500 cfm increased the percentage reduction in load by twofold. A 50% increase in base airflow rate up to 1,500 cfm, however, did not decrease the peak percentage by twofold. The drop in performance occurs when the base cfm is further increased beyond 250% and we see a drastic drop in percentage load reduction, which should begin to alarm the cost-benefit evaluation of this process. The designer should weigh the economics of the system, including the cost of installation with the actual benefits of the overall reduction in cooling load. In other words, there might be a benefit in increasing the initial value of the secondary stage airflow; however, increasing the airflow more than 50% will not be an economically justifiable heat recovery solution.Conclusion
The cool condensate from a large air conditioning process may be collected and used to reduce the cooling load in an independent and smaller air conditioning cycle. This condensate is available as free cooling since it is a byproduct that is designed to be discharged to waste. Three factors increase the energy recovery process: a location with high ambient wetbulb temperature; a primary latent cooling load large enough to produce condensate that could be used as the media of heat recovery; and a smaller secondary cooling load that is independent of the primary cycle.
Here we discussed the reduction in load at peak summer conditions. Obviously, it is expected that this system will be more attractive in locations where high wetbulb temperatures occur year-round. Piping the condensate by gravity to the secondary cooling coil adds another benefit of not utilizing motor horsepower for pumping. ES
Footnotes
1. Standard conditions indicate typical design settings at 0.4% ASHRAE summer values, 74° F indoor db thermostat setting, 25% outdoor air ratio, and 55° saturation temperature.

