FIGURE 1. Basic graphical expression for total, static, and velocity pressure in a working vent system.


The selection of a proper fan for a vent system must pursue the proper basis. This is an essential element in the engineering design phase of a vent system.

However, many controversial articles in engineering journals and other literature consider contradictive bases for selection1 through 6. Those articles notwithstanding, the natural laws of aerodynamics have strict requirements that do not allow contradictions.

This article presents graphical illustrations as the clearest demonstration of the fan selection procedure, with trade-offs between system and fan curves, air capacity and pressure, and energy consumption.

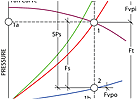
FIGURE 1A. Illustration of pressure values in the working vent system.

GRAPHICAL ILLUSTRATIONS OF AERODYNAMIC COMPONENTS IN A VENT SYSTEM

Fan and air ducts together with their associated parts comprise a vent system. Figures 1 and 1a illustrate the relationship of all existing pressures in the working system, where:

Ft - fan total pressure - system total resistance
Fvpo - fan outlet velocity pressure
Fvpi - fan inlet velocity pressure
Fs - fan static pressure
SPs - system total static pressure TPi and TPo - inlet and outlet system total pressure at a point SPi and SPo - inlet and outlet system static pressure at a point VPi and VPo - inlet and outlet system velocity pressure at a point

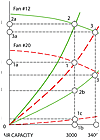
FIGURE 2. Curves of vent systems, fans, and fan outlet velocity pressures.

CONFUSION

A great deal of confusion exists in engineering literature regarding the use of static pressure. The difference in terminology and nature of the SPs and Fs is clearly illustrated in Figures 1 and 1a.

SPs = SPo-SPi7,9 Fs = Ft - Fvpo9,10 Since neither SPs nor Fs represent the amount of energy which must be imparted to the system by the properly selected fan, these two values are absolutely irrelevant as a basis for the fan selection.



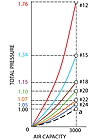
FIGURE 3. Vent system curves of the different fans.

The ASHRAE handbook states that "Fan total pressure is a true indication of the energy imparted to the air stream by the fan ... An energy loss in a duct system can be defined only as a total pressure loss ... By using total pressure for both fan selection and air distribution system design, the design engineer is assured that he is using the correct fundamentals. These fundamentals will apply equally well to both high and low velocity systems".7

However, there is apparent contradiction even in the ASHRAE handbook, such as: "System resistance to air flow is noted by total pressure ... To obtain the fan static pressure requirement for fan selection where the fan total pressure is known, use: Ps = Pt - Pv,o".8

Now, the following questions must be solved:

  • Why is this the "requirement" to obtain fan static pressure?
  • Why is it necessary to calculate the fan static pressure if the fan total pressure is already known?
  • And especially when the "total pressure ... is ... the correct fundamental[s]."7



    As described in the ASHRAE handbook, the following is a procedure for the fan selection8:

  • Determine air capacity and fan total pressure as a result of the vent system calculation.
  • Select a fan by means of the air capacity only.
  • Calculate the selected fan's outlet velocity - Vo.
  • Calculate Fvpo.
  • Calculate Fs = Ft - Fvpo.
  • Make final fan selection on the basis of the cfm and the Fs.



    TABLE 1. The NYB catalog data for fan 20 PLR. (Table courtesy of New York Blower Co., Bulletin 051.)

    This fan selection process evaluation can be better demonstrated through the use of an illustrative example, where two different sizes of fans are selected for the same 3,000 cfm at Fs = 1 in. wg (Tables 1 and 2).

    In the first case, a designer selects fan size of 20 PLR. In the second case, a contractor selects the least expensive fan size of 12 PLR (Table 2). In both instances, it appears that both fans have the same cfm and Fs, however, there is a noticeable difference in Ft pressure between the two options.

    Figure 2 is provided to illustrate the results:

    Fan 20 PLR, 3,000 cfm at Fs =1 in. wg; 1,000 rpm:

  • Parabola 0-1-3 is the characteristic of the designed or existing vent system with 3,000 cfm at Fs1 = line 1-1c = 1 in. wg.
  • Parabola 0-1c is the characteristic of the fan outlet velocity pressure Fvpo1 = line 1b-1c = 0.1 in. wg.

    Fan 12 PLR, 3,000 cfm at Fs=1 in. wg; 3,200 rpm:

  • Parabola 0-2 is the characteristic of the imaginary vent system with 3,000 cfm at Fs2 = line 2-2b = 1 in. wg.
  • Parabola 0-2b-3c is the characteristic of Fvpo2 = line 2b-1b = 0.8 in. wg.

    Fan 12 PLR, 3,400 cfm at Fs=1 in. wg; 3,200 rpm:

  • Parabola 0-1-3 is the characteristic of the designed vent system with 3,400 cfm at Fs3= line 3-3c = 0.7 in. wg.
  • Parabola 0-2b-3c is the characteristic of Fvpo3 = line 3c-3b = 1 in. Wg

    TABLE 2. The NYB catalog data for fan 12 PLR. (Table courtesy of New York Blower Co., Bulletin 051.)

    Key Point 1. Table 1, Table 2, and Figure 2 expose an error, which occurs when the Fs is applied. The fans 20 PLR and 12 PLR with the same Fs (1 in. wg) have different Ft. The fan 20 PLR has Ft = 1.1 in. wg and Fan-12 PLR has Ft = 1.8 in. wg. As a result, the real capacity of the fan 12 PLR in the vent system comes to 3,400 cfm at Ft = 1.7 in. wg and Fs = 0.7 in. wg.

    Table 3 lists fans, which were selected from fan manufacturer's data, for an air capacity 3,000 cfm at 1 in. wg Fs (Point "a").

    Figure 3 shows that each of the selected fans has a different curve for its particular individual system as compared to the designed vent system. The parabola 0-a, is the imaginary characteristic line of the designed vent system with 3,000 cfm at 1 in. wg Fs.

    Key Point 2. The artificially determined value of Fs, while neglecting the Fvpo, cannot be produced by a fan as a single value. In reality, the fan imparts in a vent system the Ft.

    Therefore, in spite of having the equal Fs and air capacity, the different fans (Table 3, Figure 3) have different Ft. Figure 3 illustrates that when a selection of fan is based on Fs, neither one of the fans satisfies the designed vent system.

    TABLE 3. The NYB catalog data for different sizes of Fans. (Table courtesy of New York Blower Co., Bulletin 051.)

    CONCLUSION

  • The article's intention is to graphically prove that Fs is an unacceptable basis for fan selection. It cannot be read directly from the calculation sheet and cannot be measured in the field.
  • In a vent system, fans do not impart only Fs as a single value. "As stated before, a fan impeller imparts static and kinetic energy to the air. This energy is represented in the increase in total pressure."7
  • The essential point is a designer must recognize that no matter what methods have been applied to calculate the vent system (equal friction, velocity reduction, static regain, or constant velocity, etc.), the result appears in value of the total pressure, not in static pressure.
  • The attention-grabbing fact is that both the pressure loss calculations and fan performance results eventuate in a value of the total pressure. Thus, fan total pressure, evidently and logically, is the only proper basis for the fan selection.
  • As the essential energy saving measure, the fan manufacturers must provide graphs, illustrating system / fan trade-offs: fan curves, air capacity and total pressure, mechanical efficiency, energy consumption, and noise levels. ES