During the mid-1990s, Ron Michael, regional manager, Loren Cook Co., was conducting a lunch and learn at a large engineering firm on the East Coast. As talk turned to fan selection and use of Cook’s software program, Michael was interrupted by the head of the firm’s mechanical department.
“Show us how to read a fan curve,” the head of the mechanical department requested.
Being new to the field, Michael assumed every engineer — especially ones at such a large firm — knew how to read a fan curve, the graphical representation of a fan’s performance, specifically noting the relationship between the amount of airflow and the amount of static pressure produced.
“My first thought was he actually wants to see if I know how to read a fan curve,” Michael recalled. “So, I began my presentation in detail, knowing I could not screw this up.”
A few minutes into Michael’s explanation, the head of the mechanical department interrupted again.
“We don’t have that much time, based on our busy schedules, so we use the rule-of-thumb method.”
“The rule-of-thumb method?” Michael asked.
This involves placing the palm of one’s left hand on a fan-curve graph so that the index finger is aligned with the left vertical (y-) axis, along which static pressure is plotted, and the thumb is aligned with the horizontal (x-) axis, along which air-volume flow rate is plotted (more on this later), the head of the mechanical department explained. Where a vertical line extending upward from the tip of the thumb intersects the flow-versus-pressure curve is the fan’s operating point (again, more on this later) (see Figure 1).
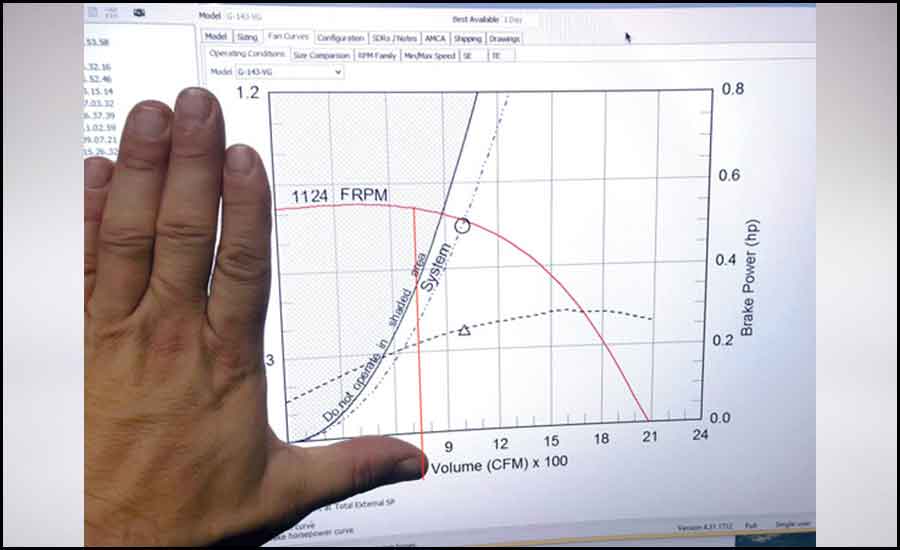
FIGURE 1: The so-called rule-of-thumb method.
“I didn’t quite know what to say but quickly determined that not many people in the room actually knew how to read a fan curve,” Michael reminisced.
Those people were hardly alone and would not be lacking company today. While, at first glance, a fan curve can appear complicated, it is fairly easy to interpret once one gains an understanding of the conventions and terminology used. Reading a fan curve (correctly) is a skill worth possessing, as it allows those who select and specify fans to understand the performance characteristics and capabilities of different equipment so they may determine the fan that best suits the requirements of an application. For them, this article will help to straighten out fan curves.
While there is no standard method for graphically representing fan-performance data, this article will cover what one is most likely to see.
Airflow and Pressure Loss
In the design of a ventilation system, the desired airflow rate and system pressure loss (static pressure or total pressure) often are referred to as the duty point. A fan curve depicts duty point.
As stated earlier, on a fan-curve graph, airflow — typically expressed in cubic feet per minute (cfm), cubic meters per second (m³/s),¹ cubic meters per hour (m³/h), or liters per second (l/s) — is represented along the x-axis, while system pressure loss — typically expressed in inches of water gauge (in. w.g., or in. H2O), Pascals (Pa)¹, or millimeters of water gauge (mm H2O) — is represented along the left, y-axis.
In the succeeding examples, the desired airflow and system pressure loss are 12,000 cfm (5.66 m³/s) and 5.0 in. w.g. (1,244 Pa), respectively (see Figure 2).

FIGURE 2: Duty point of 12,000 cfm (5.66 m3/s) at 5.0-in.-w.g. (1,244 Pa) system pressure loss.
Fan Selection
Whether via the internet, on the company's website, or as a program to be installed on a user’s computer, many fan manufacturers offer software capable of quickly identifying a number of possible fan solutions for a given duty point. Typically, possible fan selections are displayed in a table showing model type, size, flow, pressure, speed, required power, efficiency, outlet velocity, and other relevant data.
Table 1 shows output from one program for our duty point of 12,000 cfm (5.66 m³/s) at 5-in.-w.g. (1,244 Pa) static pressure. The seven selections are for one model type, GI Cent., and one wheel type, AF. A manufacturer’s selection program may yield many more options.
All of the selections in Table 1 are capable of achieving the duty point in our example.
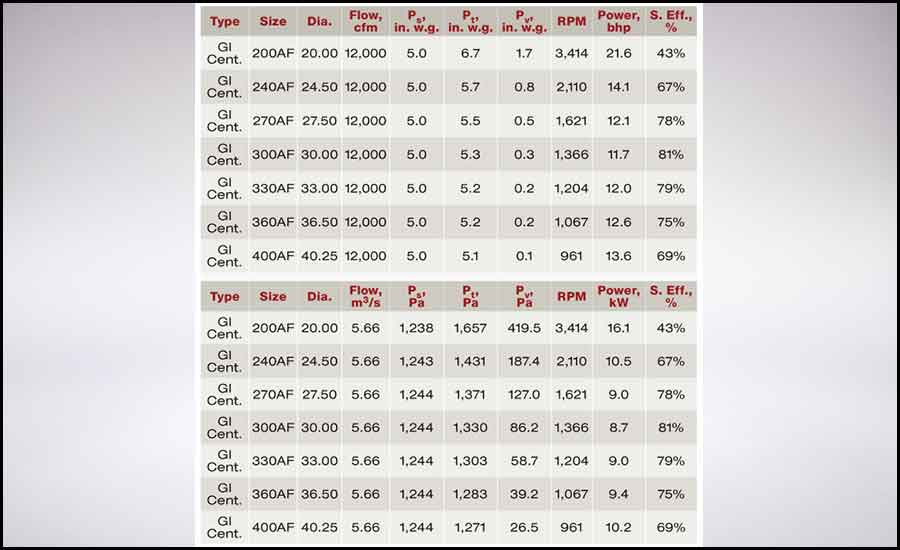
TABLE 1: Typical fan-selection table.
Fan Performance Curve
The first point on our graph is the duty point: 12,000 cfm (5.66 m³/s) at 5-in.-w.g. (1,244 Pa) static pressure. Adding data showing fan flow and pressure at points other than the duty point produces the first curve, shown in black in Figure 3.

FIGURE 3: A flow-versus-pressure curve.
To read the curve, draw or imagine a line extending vertically from the required flow on the x-axis up to and slightly through the curve (the yellow dashed line in Figure 3). From that intersection of line and curve, draw or imagine a line extending horizontally to the y-axis to determine the pressure produced by the fan (the blue dashed line in Figure 3). This should be the required pressure. In Figure 3, the fan flow curve intersects the duty point at the desired flow and pressure, as required.
Typically, the power required by the fan is also displayed. A power curve can be shown on the left or the right axis and should be read at the required flow. In Figure 4, draw or imagine a line extending from 12,000 cfm (5.66 m³/s) on the x-axis straight up to the red power curve. From there, read horizontally to the right to determine the power required by the fan. In this case, the required power is 11.7 bhp (8.7 kW).
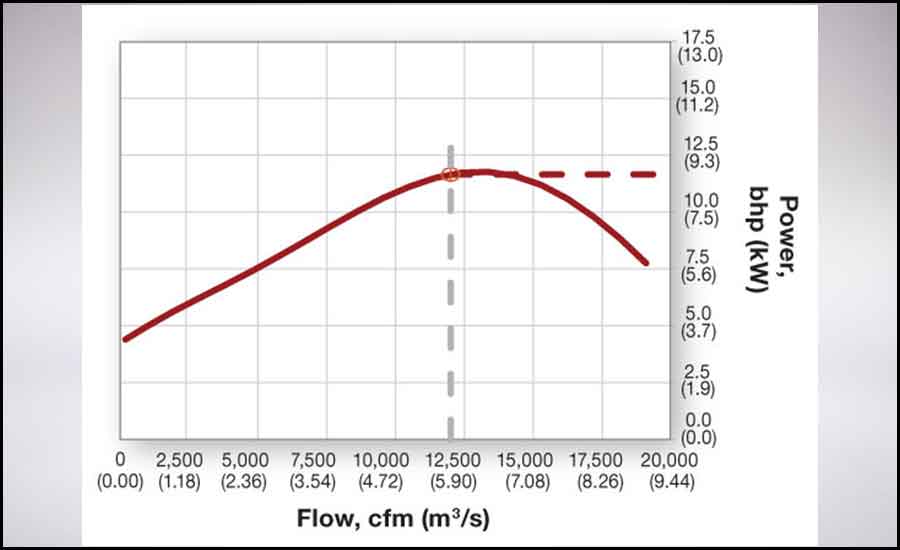
FIGURE 4: A flow-versus-power curve.
Generally, the power required by a fan increases as flow through the fan increases. With many airfoil and backward-curved or backward-inclined fans, however, power reaches a peak value and then decreases as flow increases.² This type of power curve is known as “non-overloading.” If the driving motor power is greater than the peak power on the curve with allowances for temperature and drives, etc., the fan should not overload in operation.
The power curves of many axial propeller fans and ventilators will show power decreasing as flow increases to the point of free delivery.²
Though flow-versus-power curves can be shown on a separate graph, typically they are superimposed with flow-versus-pressure curves on the same graph, with pressure along the left axis and power along the right (see Figure 5).
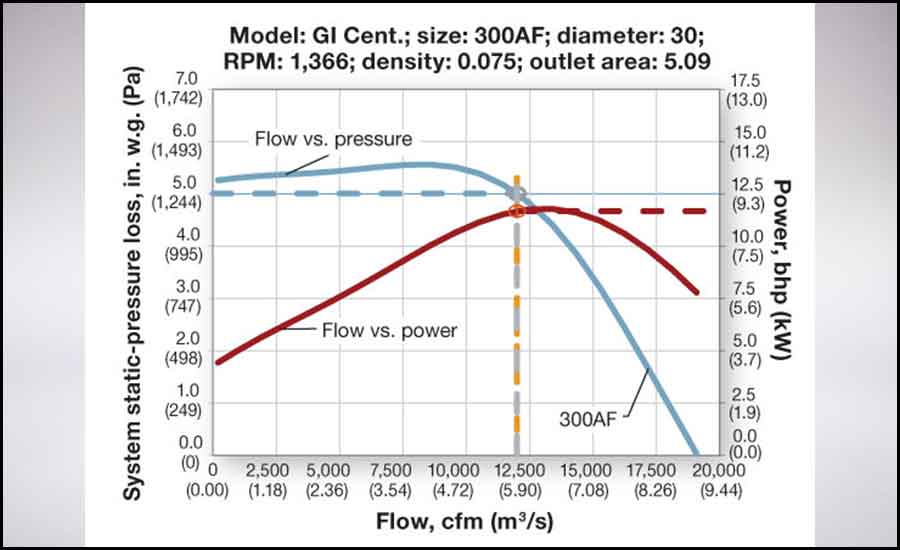
FIGURE 5: Superimposed flow-versus-pressure and flow-versus-power curves.
Figure 5 includes additional information necessary on a fan-curve graph: fan model, fan size, or diameter (both included here); revolutions per minute (RPM); air density; and outlet area.² Outlet velocity may be provided in lieu of outlet area.
In the case of most industrial exhausters, pressure and combustion blowers, and forward-curved fans, the power curve increases as flow increases to the point of free delivery.² Figure 6 is the fan-curve graph for an industrial exhauster selected for our example duty point. This selection is much less efficient at 14.4 bhp (10.7 kW). The peak power on the power curve is about 20.5 bhp (15.3 kW). The graph includes additional notes regarding how the fan was tested and the performance and power losses that are included. In this case, the test was ducted inlet and ducted outlet. The fan installation should be similar to the test setup to avoid system effects. The power ratings do not include drive losses; V-belt-drive losses will have to be added to the power requirement for the motor.
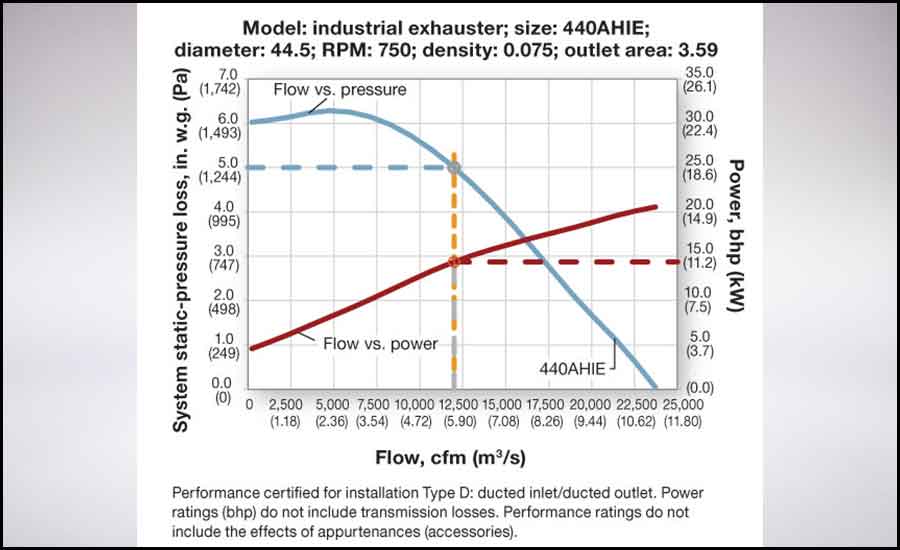
FIGURE 6: An industrial exhauster with increasing power.
A quick review of the fan curves of the seven fan selections in our example narrows the field of acceptable options. In Figure 7, the flow-versus-pressure curve of each selection is superimposed on a single graph. Generally, a fan will exhibit some degree of flow and pressure instability to the left of peak pressure. A fan’s operating point should be to the right of peak pressure. Using 95% of peak pressure as a guide for selection in this case eliminates the 400AF and 360AF selections. Most manufacturers’ software will identify, or not select, fans to the left of or near peak pressure.
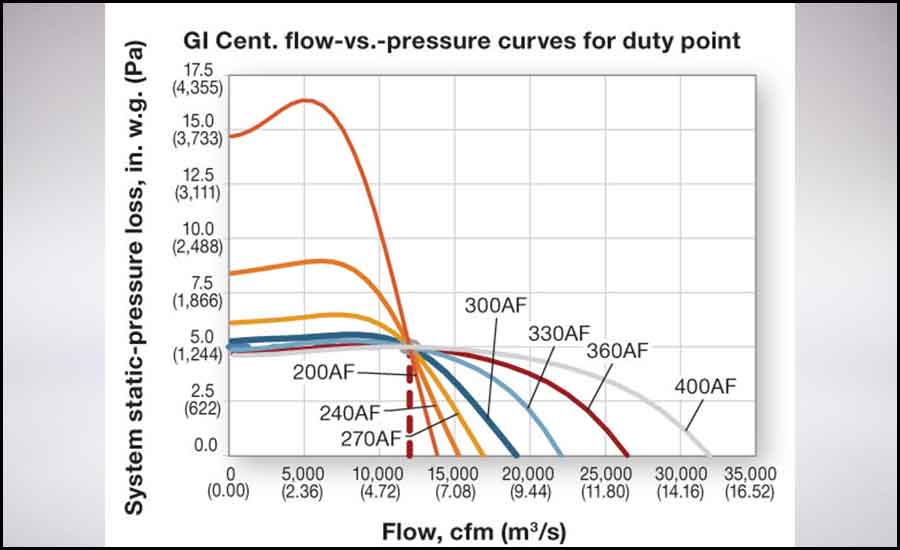
FIGURE 7: Flow-versus-pressure curves.
Smaller fans operating at lower efficiencies can be found closer to free delivery, farther to the right than other selections, on the fan curve. In this case, the 240AF selection is operating to the right, while the 200AF selection is operating far to the right.
Static- and Total-Pressure Curves
Corresponding to average air velocity at a specified fan outlet, fan velocity pressure is added to the fan static pressure at each flow point to develop the fan-flow-versus-total-pressure curve.³ Fan total pressure is equal to the sum of fan static pressure and fan velocity pressure. In Figure 8, the total-pressure curve is shown by the dashed blue line. In this example, the outlet velocity for the 300AF fan is 2,359 fpm (12 m/s), the velocity pressure is 0.35 in. w.g. (86 Pa), and the total pressure is 5.35 in. w.g. (1,331 Pa) at the flow point of 12,000 cfm (5.66 m³/s).
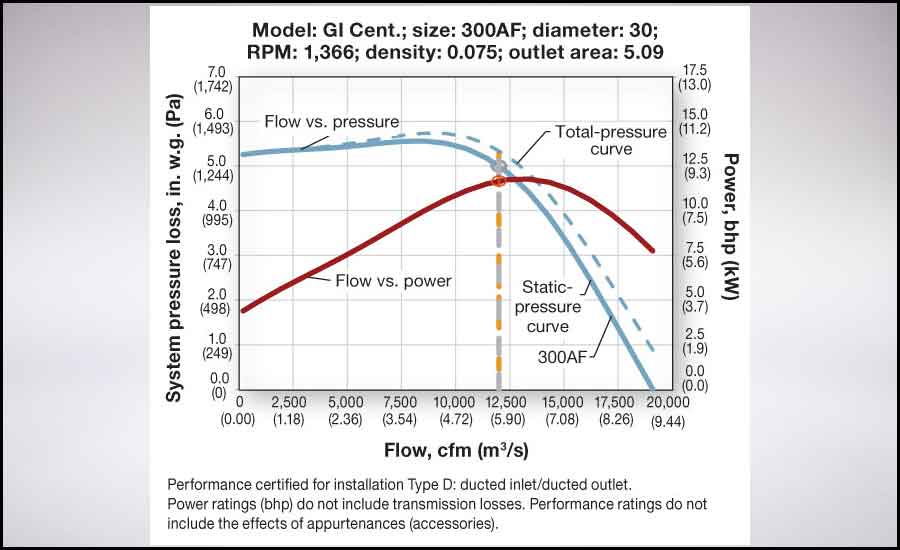
FIGURE 8: Flow-versus-static and total-pressure curves
The required system velocity may be determined based on the approximate duct size for the flow. Lower velocities require larger ducts, which, of course, take up more space. Higher velocities require smaller ducts, which often produce more noise. Other factors, such as cost, space, and conveying velocity, are important considerations when determining velocities.³
Fan Efficiency
Flow-versus-static-efficiency or flow-versus-total-efficiency curves also are included on many performance graphs. Scaling the display of efficiency-curve values to match the displayed power- or pressure-scale value can be challenging. In Figure 9, the static-efficiency curve is the light blue line. At 12,000 cfm (5.66 m³/s), the static-efficiency value is 81.1% (8.11, 811% × 0.1), scaling factor from the right axis. The total efficiency is 86.8%. In this example, the fan is selected just to the left of peak efficiency.
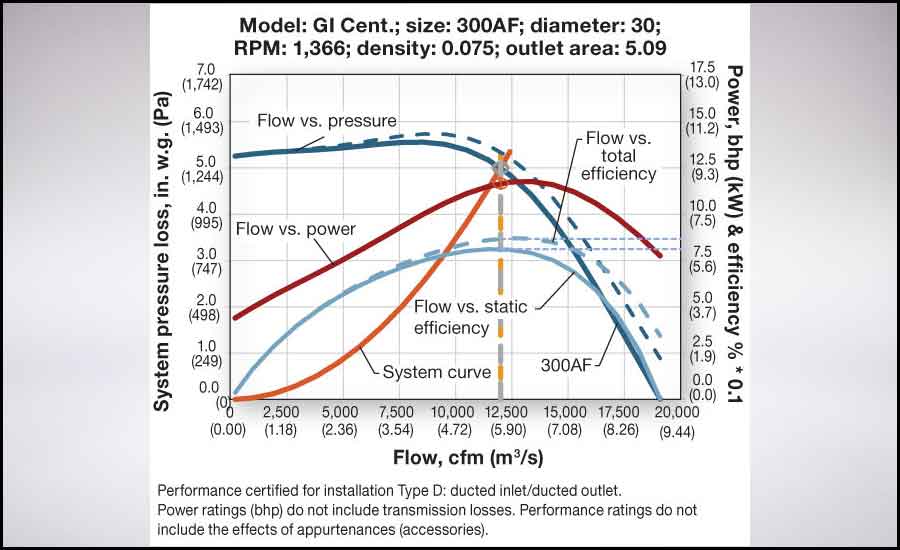
FIGURE 9: Flow-versus-static-efficiency, flow-versus-total-efficiency, and system curves.
System Curve
Figure 9 also includes an orange parabola representing system resistance at various flows. Resistance generally varies as the square of flow ratio.² The fan will operate at the intersection of the system curve and the fan curve.⁴
Conclusion
This article covered some of the most commonly encountered fan curves. There are additional curves with multiple speeds, multiple blade angles, and combinations of fan performance data. Curves with fan energy index (FEI) operating bubbles,⁵ motor-sizing limits, inlet-turning-vane data, and other information are derived from the curves shown here. Knowing to start at the required system flow and work up to the pressure, power, efficiency, or system curve is the key to untangling fan curves.
This article originally appeared in the 2020 edition of AMCA inmotion magazine.
References
1. AMCA. (2016). Standards handbook. ANSI/AMCA Standard 99. Arlington Heights, IL: Air Movement and Control Association International.
2. AMCA. (2002). Fans and systems. AMCA Publication 201. Arlington Heights, IL: Air Movement and Control Association International.
3. ACGIH. (2019). Industrial ventilation: A manual of recommended practice for design (30th ed.). Cincinnati: American Conference of Governmental Industrial Hygienists.
4. AMCA. (2011). Air systems. AMCA Publication 200. Arlington Heights, IL: Air Movement and Control Association International.
5. AMCA. (2018). Calculation of the fan energy index. ANSI/AMCA Standard 208. Arlington Heights, IL: Air Movement and Control Association International.





