The formula was revised to improve its accuracy, especially at off-design conditions. The goal was to give chiller buyers better information with which to make energy comparisons.
However, the revised formula was derived from analysis of a single-chiller system. This has raised concerns about its applicability to multiple-chiller systems, which make up the majority of chiller plants. This article will explain the components of the formula, what makes multiple-chiller systems different from single-chiller systems, and why the formula works for both types.
Background
ARI Standard 550/590-98 uses a formula to calculate average chiller efficiency. The formula uses a set of four operating conditions. Each condition consists of a "% design load" and a "head."The head is represented by either an outdoor drybulb (db) temperature for air-cooled chillers, or an entering condenser water temperature (ECWT) for water-cooled chillers. For water-cooled chillers, the four conditions are 100% @ 85°F ECWT, 75% @ 75°F ECWT, 50% @ 65°F ECWT, and 25% @ 65°F ECWT. These temperatures were derived by averaging weather data from around the United States and using a typical cooling tower approach.
The formula then makes some assumptions about chiller operating hours. It assumes that a chiller spends 1% of its operating hours at 100% load and 85°F ECWT simultaneously, 42% of operating hours at 75% load and 75°F ECWT, 45% of operating hours at 50% load and 65°F ECWT, and 12% of operating hours at 25% load and 65°F ECWT. These values are based on weather data, recognizing the major impact of weather on both chiller loading and efficiency.
The result of the formula is a chiller-efficiency number expressed in kW/ton. If the chiller design conditions are the standard ARI conditions (44°F leaving chilled-water temperature, 85°F ECWT or 95°F outdoor db, 2.4 gpm/ton evaporator flow, 3.0 gpm/ton condenser flow, and standard fouling factors), then the efficiency number is known as the integrated part-load value (IPLV).
If chiller design conditions are anything other than the standard ARI conditions (83°F ECWT or different flow rates), then the efficiency number is known as the nonstandard part-load value (NPLV). IPLV is a specialized subset of NPLV, and is used primarily in manufacturers' catalogs. We will use the broader measurement of NPLV in this article.
ARI recognizes that an NPLV rating can't predict exactly what the absolute chiller efficiency would be in an actual installation. NPLV does, however, provide a meaningful way of comparing the relative efficiency of different chiller models. The actual efficiency may differ from the NPLV by a few percentage points, but each chiller model will differ by a similar amount.

Multiple-Chiller Question
Standard 550/590-98 states that NPLV applies to single-chiller systems and that full energy analyses should be used for multiple-chiller systems. ARI recognized that multiple-chiller systems make up the majority of chiller plants. However, single-chiller plants are easier to analyze, so ARI started there. Multiple-chiller plants are currently under study by ARI.However, an independent study, conducted by York International (York, PA), concludes that the new standard also tracks the efficiency of chillers in multiple-chiller configurations.
What makes multiple-chiller plants different from single-chiller plants, as far as chiller efficiency is concerned?
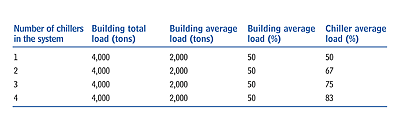
In a single-chiller plant, the chiller sees the full range of building cooling loads, from 100% design load down to 10%, when the chiller shuts off. In multiple-chiller systems, on the other hand, chillers cycle off as the building's cooling load gets lower, and the load on the remaining chillers increases. The result is that the individual chillers see higher loads on average. In fact, the more chillers there are in the system, the higher the average chiller load. (Table 1 illustrates this phenomenon.)
A multiple-chiller system appears to breach the assumptions used in calculating NPLV. The weather assumptions would be fundamentally unchanged, but the chiller-loading assumptions would change, with more hours being spent at higher loads.
Wouldn't this make the standard and NPLV inapplicable for multiple-chiller systems?
Multiple-Chiller Answer
Surprisingly, no. NPLV is also valid for multiple-chiller systems, despite the difference in average chiller loading. In analyzing these systems, it was discovered that the standard does accurately predict chiller efficiency for multiple-chiller systems.How can that be, if the assumptions used in the formula have changed so radically? To find the answer, we need to look at the factors that determine the efficiency of a refrigeration compressor.
There are two factors: load and head.
Load is the amount of refrigerant gas that the compressor must handle over time. Head is the pressure difference against which the compressor must operate. In a water chiller, the lower pressure is determined by the evaporator temperature. The higher pressure is determined by the condensing temperature, which is determined primarily by the weather conditions (the outdoor drybulb temperature entering the air-cooled condenser, or the wetbulb temperature of the air entering the cooling tower).
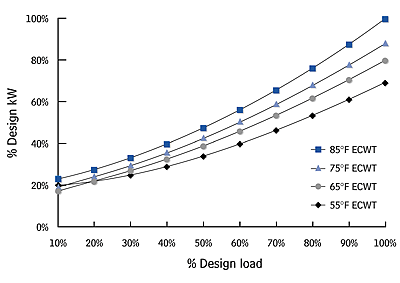
Which has the greater impact on compressor efficiency, load or head? Let's look at water-cooled centrifugal chillers, the most common type used in large plants. Figure 1 shows the energy performance of a "typical" centrifugal chiller. The performance was simulated by averaging together the most recent performance curves published by York International, Carrier Corp. (Syracuse, NY), and The Trane Company (La Crosse, WI) in their respective catalogs. The curves show the relationship between "% design load" and "% design kW" for various ECWTs.
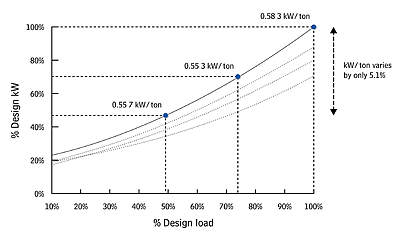
If we hold the head constant (by using only the 85°F ECWT line) and vary the load, what happens to chiller efficiency? We find that the kW/ton varies relatively little - only 5%. (This is illustrated in Figure 2, using the same curves as in Figure 1.)
A simple analogy may help clarify why the change is so small. Imagine a catapult (representing the compressor) throwing a 10-lb rock (the load) up a 20-ft cliff (the head). Say that the power required for this operation is 1 hp. If the rock only weighs 5 lb, then the machine only needs 0.5 hp.
Is the machine becoming more efficient in hp/lb? No. If we divide power (hp) by load (lb), we get the same answer in both cases: 1 ÷ 10 = 0.5 ÷ 5 = 0.1 hp/lb. Alternatively, if we hold the load constant (at 100%, for example) and vary the head, we find that change in chiller efficiency can be as much as 30%. (This is illustrated in Figure 3.) Let's use our same simple analogy to examine this case. Imagine the rock (the load) stays at 10 lb, but the cliff (the head) is lowered to 10 ft. Now the catapult would require 0.7 hp to accomplish the operation.
Has the catapult become more efficient? Yes. If we divide the power (hp) by the load (lb), the answer is now 0.7 ÷ 10 = 0.07 hp/lb, which is 30% better than when we only lowered the load in Figure 2.
We said earlier that the chiller-loading pattern in a multiple-chiller plant is different than a single-chiller plant. However, the weather stays the same, no matter how many chillers are in the plant. Because head (determined by weather) will have the most impact on chiller efficiency, and load (determined by the number of chillers) will have a relatively minor impact, it stands to reason that ARI 550/590-98 will accurately predict chiller efficiency in multiple-chiller plants.
Let's analyze a multiple-chiller plant and see if that is true.

Analysis Of A Multiple-Chiller Plant
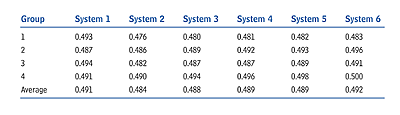
Six systems were analyzed, addressing the same building load, using from 1 to 6 chillers each, using average U.S. weather data, and run with four different operating schedules.
Group # Description of operating schedule
1 24 hr/day, 7 days/week, chiller shut off below 0°F outdoor db
2 24 hr/day, 7 days/week, chiller shut off below 55°F outdoor db
3 12 hr/day, 5 days/week, chiller shut off below 0°F outdoor db
4 12 hr/day, 5 days/week, chiller shut off below 55°F outdoor db
The building load parameters used were:
- Design building cooling load = 3,600 tons
- Design outdoor db temperature = 100°F
- Design outdoor wb temperature = 78°F
- Design cooling tower approach = 7°F
- Design efficiency for all chillers = 0.583 kW/ton
- NPLV for each chiller (as predicted by ARI 550/590-98) = 0.488 kW/ton
- Design leaving chilled-water temperature = 44°F
- Minimum entering condenser-water temperature = 65°F
- Average internal load = 40% of peak
System # Description of chiller system
(all constant-speed)
1 One 3,600-ton unit
2 Two 1,800-ton units
3 Three 1,200-ton units
4 Four 900-ton units
5 Five 720-ton units
6 Six 600-ton units
From this information, 24 analyses were created using the ASHRAE temperature-bin method for calculating energy. (The results are summarized in Table 2.)
The results show that the average kW/ton for single- and multiple-chiller systems are the same, within reasonable accuracy. The new NPLV rating tracks efficiency for multiple-chiller systems as well as single-chiller systems. (Full data from this analysis is available from York.)
Summary
ARI Standard 550/590-98 states that NPLV is applicable to single-chiller systems because of its chiller-loading assumptions.However, it turns out that the standard is equally applicable to multiple-chiller systems because chiller loading (between 50% and 100% load, where individual chillers operate in multiple-chiller systems) only marginally impacts chiller efficiency.
The major factor in chiller efficiency is head, which is determined by the weather. And the weather doesn't care how many chillers a plant contains.ES
