
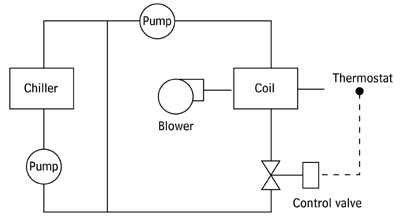
One can easily see from Figure 1 that the control valve is the key link between the temperature of the building and the operation of the hydronic system. Unfortunately, valves are sometimes sized in the vacuum of a design basis. The manners in which the valve must interact with other equipment, maintenance needs, demand surges, and future expansion possibilities are often overlooked.
These are just some of the factors which cannot be overlooked, says Anthony McGuire of McGuire Engineers (Chicago). It is his belief that conscientious designers should think years ahead for the industrial building (and the process systems) they are designing.
"As an example, Chicago is presently seeing warehouses, loft manufacturing facilities, and office buildings being converted into housing and offices," he says. "The basic system needs to have some level of flexibility. The level required for a specific project can vary widely for any number of reasons - client finances, user criteria, and so forth. The designer needs to understand the overall picture in order to develop a proper system configuration."
In other words, it is important for the hvacr engineer to keep in mind that the control valve is an integral part of a larger system.
The Hydraulics Of Control Valve Sizing
Theoretically, the control valve is treated as a simple restriction in the liquid piping (Figure 2). As the flow approaches the restriction, the system (or dynamic) pressure of the system begins to drop dramatically. The system (or dynamic) pressure reaches its lowest value shortly after the restriction. At a distance of about 8 pipe diameters downstream of the restriction, the system (or dynamic) pressure is almost completely recovered. Some pressure is lost due to friction and turbulence.In essence, the fluid's dramatic drop in pressure during its approach to the restriction is an indication that the potential energy of the fluid is being converted into kinetic energy. That is, the pressure-related energy of the fluid is being converted to velocity-related energy. The fluid accelerates as it approaches the restriction and hits a maximum velocity at the point where the fluid has the lowest static pressure. As the pressure is recovered, the fluid slows in velocity and resumes its original speed.
Equations for control valve sizing are developed from the first law of thermodynamics. The control valve is approximated as an adiabatic, irreversible flash. This can be restated as an isenthalpic or constant enthalpy process, when kinetic effects are negligible. As can be seen in Figure 2, the flow experiences an expansion after passing through the line restriction. This type of expansion is referred to as a Joule-Thompson expansion.
Applying the first law of thermodynamics to a control valve, one derives a very useful equation applicable for design. The governing equation used in control valve selection and sizing is presented here:
Q = Cv square root P1 - P2
where Q is the volumetric flow rate, P1 is the upstream pressure, P2 is the downstream pressure, and CV is the flow coefficient.
In practice, the above equation is rearranged as the following for easy usage:
CV = _Q___
square root P1 - P2
With the second equation, the designer can determine the CV required of the control valve for a specific design case. The CV as determined in Equation 2 is then compared to the CV values as published by manufacturers for a given valve at a given pressure drop. For good control, the required CV should fall between 70% to 90% of the control valve's maximum CV capability.
Improperly Sized Valves Based On Incorrect CV
A common problem in control valve sizing is to oversize a valve based on the use of a safety factor. For instance, suppose that the process in question requires a maximum CVof 2.5. The engineer then checks the valve manufacturer's catalogue and sees that a valve is available with a maximum CVof 2.5. However, to be on the safe side, the engineer then adds a safety factor of 20%, which boosts the valve's maximum CVto 3.0. Thus, the valve selected is the valve with the next highest rating. (In this example, it's a CVof 4.0.)
The problem with this is that the valve is now excessively oversized. The ratio of the maximum CV of the valve per the maximum CV required should never exceed 1.6. The equation (hereby identified as Equation 3) is as follows:
CR = maximum value CV <1.6
maximum required CV
In the above example, CR = 4.0/2.5 = 1.6. Oversizing a valve due to the use of a safety factor can lead to premature valve failure. Such failures are usually manifested in the seat, packing, and the actuator.
Randall Amerson of Siemens Building Technologies (Buffalo Grove, IL) says the net effect of this is that the actual range of control for the valve in terms of its stroke or rotation is significantly reduced compared to the design case.
"In severe cases, this phenomenon can accelarate the wear of the stem packings and the erosion of the valve trim due to control cycling and continuous valve operation near the seat," he says. "The operating life of the associated valve actuator may also be shortened as a result.
"Suffice to say that careful attention to details and product design specifications can enhance the performance of hvac control valves in real-world applications."
Thus, the engineer most keep two things in mind when sizing and selecting a control valve. First, for proper control, the required CV of the process must fall between 70% to 90% of the control valve's maximum CV range. Second, to ensure proper control valve selection, the value of CR in Equation 3 noted above must be less than 1.6. These two stipulations, when applied together, provide good control and prevent premature valve failure.
Linearizing The Relationship
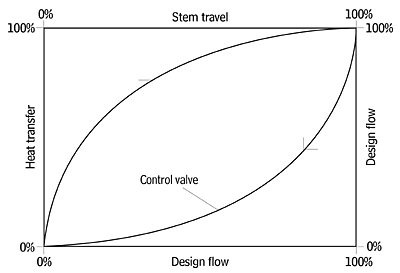
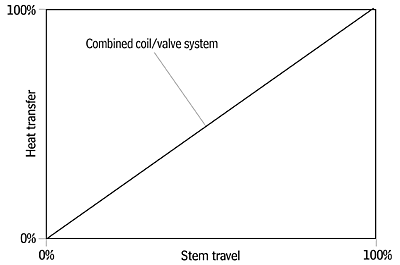
Linearized relationships are always valued in control systems. Such correlation between input and output produce tighter and finer control. For this reason, a designer should specify a control valve with equal percentage flow characteristics. The net effect of the selection is to linearize the relationship between heat transfer and stem travel.Figure 3 is a simplified diagram showing how coils and valves operate. Coils exhibit a heat transfer relationship that varies closely with the square root of the flow. On the other hand, the control valve (equal percentage) exhibits a flow characteristic that varies nearly to the square of the stem travel. When the coil and the equal percentage control valve are connected in the control loop, the net effect is a linear relationship between heat transfer and stem travel (Figure 4).
Chicago consultant Richard Hegberg points out that "harmonizing the relationship between coil and valve not only leads to better control, but to higher customer satisfaction, for deviations from the setpoint can surely be noticed by the occupants of the building."
Kathleen Langelund, of Siemens Building Technologies, adds that the coil and its control valve contribute to the space conditions of a building, but their importance is sometimes overlooked in sizing a large system.
"Everyone knows how important it is to get the right size chiller in a building, but its sizing will not be considered as correct if the space temperature setpoint is not satisfied," she says.
It is very clear that an hvacr engineer cannot simply size the control valve based on a mere data sheet, ignoring the process and the equipment. Rather, as Hegberg and Langelund point out, the coil and the valve are integral parts in providing the client with the desired product: comfortable building temperature and humidity. Therefore, both coil and valve must be sized properly with respect to one another.
Computer Modeling
The proper design of a hydronic system is a difficult and complex task. Many different aspects of the job must be considered carefully: piping velocities, pipe sizes, equipment and pipe pressure drops, pump sizing and curves, piping networks, etc. Unfortunately, these tasks are carried out semi-independently from one another. They should be considered simultaneously, since the entire system must operate as a complete unit."Computational system modeling is certainly not a new concept, but there were no easy-to-use tools available until recently," says Tom Glassen, of Applied Flow Technology (Woodland Park, CO). "With the availability of significantly powerful desktop computing hardware, this situation has changed. Several firms have produced good modeling software designed specifically for piping systems."
He adds, "Traditional tools used for the design and analysis of piping systems include spreadsheets for piping pressure drop calculations and data for the selection of pumps and control valves. But these tools are disconnected, making a comprehensive and quantitative exploration of operating conditions and equipment in a system time consuming. Often, it is simply not done.
"System modeling software does not replace traditional engineering design methods; rather, it connects all of the methods in an integrated system and allows the design to be simulated as an actual, linked process. This improves the quality of specification and is particularly beneficial to flow control devices."
Hegberg agrees that modeling software is extremely useful in the design of direct and reverse-return pressure distribution systems.
"This is especially true when one considers that each circuit in the process must be thoroughly analyzed for proper hydraulic flow: pump, supply main, terminal, control valve, balancing device, fittings, and return main," says Hegberg.
Throughout a hydronic design project, the system flow resistance is constantly being changed due to modifications in pipe sizing. In addition, the pipes are constantly being rerouted due to design changes (for instance, tapping into headers at different locations and diverting flow around building pillars, beams, and equipment). Changes in pipe sizes and pipe networks change both the system flow resistance and, thereby, the operation of the pump and the required pressure drop across the valve. The control valve is usually seen as taking up the excess pressure provided by the pump. Therefore, the pump and the control valve must be sized with each other in mind.
One rule of thumb: The system resistance should intersect the pump curve at, approximately, a 45-degree line from the origin. (However, keep in mind future expansion possibilities, too.) A system resistance curve that is too low or too steep can result in inefficient pump performance and even mechanical failure (shaft, bearings, and seals). The control valve is part of the system resistance and also affects the pump's operating point. All things considered, fluid flow modeling software makes good sense when sizing both the pump and the control valve for proper operation in light of piping changes
"Prior to making major modifications to an existing piping system, or designing a new system, it is a good idea to create a computerized hydraulic model of the hvac piping system," says Ray Hardee of Engineered Software (Lacey, WA). "Piping design and analysis software can provide information needed to properly select the pumps and control valves. In addition, the computer model system provides a good understanding of the interaction between pumps, pipelines, and control valves."
Conclusion
The sizing and selection of flow controls is a highly important task in the scope of an hvac industrial project. The valve itself must be properly sized for its design flow conditions. Moreover, it must be engineered in a manner that takes the entire system into account. Often, this is not done. The reasons are mostly related to costs and the availability of engineering workhours.A greater awareness of the importance of designing flow controls within an integrated flow system is of paramount significance. Furthermore, the tools needed for accomplishing this task are becoming much more available.
"Flow control devices have been viewed for the past 20 years as commodity items," says McGuire. "This created a situation where little thought is given to the means and methods used for flow control. Cost-sensitive owners and developers will set a lower priority on flow than other items in a project. When budgets cannot be met, alternatives are taken to reduce cost.
"Flow control devices are one of those that get hit pretty bad since the advent of 'value engineering.' Flow control is very important, but it is susceptible to deletion in the course of a project. Engineers must put it in its proper perspective." ES
